前提知識と準備
Groth16を理解するために必要な前提知識と、数学的な表記法について説明します。計算機科学を専攻している方なら当たり前である内容も多いと思います。専攻していなくても、このページは軽く流し読みして後でその概念に関してしっかり理解したくなったタイミングで読めば大丈夫です。また、全く読まなくても、意味がわからない用語が出てきたときにこのサイトの上部にある検索バーで検索すれば、このページを含めて様々なページの該当箇所がヒットするので、そこで初めて読んでみるといった進め方もできます。
アルファベット、文字、文字列、言語
アルファベットを任意の空でない集合とし、文字をアルファベットの元とし、文字列を文字からなる列とし、言語を文字列の集合とします。
アルファベット \(\lbrace 0,1 \rbrace\) から作られる任意の文字列から成る言語を \(\lbrace 0,1 \rbrace ^*\) と表します。また、この言語の文字列をバイナリ列と呼びます。バイナリ列の長さを \(n\) に限定した場合、その言語を \(\lbrace 0,1\rbrace ^n\) と表します。例えば、 \(01011 \in \lbrace 0,1\rbrace ^5\) です。
確率的多項式時間アルゴリズム
アルゴリズムの入力と出力をバイナリ列とします。
「アルゴリズム \(A\) が多項式時間アルゴリズムである」とは、 入力を \(x\) とし、その長さを \(|x|\) として、アルゴリズム \(A\) を実行するステップ数が \(|x|\) の多項式で抑えられることを意味します。
「アルゴリズム \(A\) が確率的アルゴリズムである」とは、アルゴリズム \(A\) がその内部で適当な長さの乱数を使用して、実行結果がその乱数に依存して決まることを意味します。逆に、確率的アルゴリズムではないアルゴリズムを決定的アルゴリズムと言います。
「アルゴリズム \(A\) が確率的多項式時間アルゴリズムである」とは、アルゴリズム \(A\) が多項式時間アルゴリズムかつ確率的アルゴリズムであることを意味します。
以下、確率的多項式時間アルゴリズムという記述があれば、暗に「効率的に実行できる」という意味を含んでいると考えてください。
関数のnegligibleとoverwhelming
安全性の定義や証明にnegligibleな関数やoverwhelmingな関数が使われます。これらの関数は、次のように定義されます。
negligibleな関数
自然数の集合を \(\mathbb{N}\) とし、 \(0\) 以上 \(1\) 以下の実数区間を \([0,1]\) とする。関数 \(\varepsilon: \mathbb{N}\to [0,1]\) が次の式を満たすとき、その関数はnegligibleであるという。
すなわち、negligibleな関数とは、どれだけ大きな実数 \(c\) でも、ある実数 \(k\) が存在して、 \(k\) 以上の全ての \(n\) に対して、 \(\varepsilon(n)\) は \(1/n^c\) より小さい関数である、ということです。直感的には、関数 \(\varepsilon\) はどんな多項式関数の逆数よりも小さい関数である、ということです。
逆に、「関数 \(\kappa:\mathbb{N} \to [0,1]\) がoverwhelmingである」とは、 \(1-\kappa\) がnegligibleな関数であることと定義します。
また、簡略的に \(f(x)\) がnegligibleであることを \(f(x) \approx 0\) 、 \(f(x)\) がoverwhelmingであることを \(f(x)\approx 1\) と表記することにします。
安全性の議論において、 \(\lambda\) をセキュリティパラメーター(イメージとしては鍵などのビット数)として、「この確率が \(\varepsilon(\lambda)\) より小さいなら安全だよね」あるいは「この確率が \(\kappa(\lambda)\) より大きいなら安全だよね」というような主張に使います。または、これは「 \(\lambda\) が大きくなればなるほど安全性が期待できるよね」ということも意味します。
確率変数、アンサンブル
有限集合 \(\Omega = \lbrace x_1,\ldots,x_n\rbrace\) と、 \(0\) 以上 \(1\) 以下の実数空間 \([0,1]\) において、関数 \(p:\Omega \to [0,1]\) で、
を満たすものを考えます。このとき、 \(\operatorname{Pr}[X=x] = p(x)\) となるような変数 \(X\) を確率変数と呼びます。また、有限集合 \(\Omega\) を標本空間と呼び、関数 \(p\) を確率分布と呼びます。
例えばコイントスで、表が出ることを \(1\) 、裏が出ることを \(0\) として定義すると、 \(\Omega = \lbrace 0,1 \rbrace\) であり、 \(p(0)=p(1)=\frac{1}{2}\) であり、 \(\operatorname{Pr}[X = 0] = \operatorname{Pr}[X = 1] = \frac{1}{2}\) です。
確率変数は数学的には関数であり、上記では \(X : \Omega \to \Omega\) となっていますが、正確にはある標本空間 \(\Omega\) から実数 \(\mathbb{R}\) への関数として定義されます。例として \(n\) 回のコイントスを考えてみます。標本空間 \(\Omega\) を \(\lbrace 0,1 \rbrace^n\) とします。バイナリ列 \(x = (x_1,\ldots,x_n) \in \Omega\) は、コインを \(n\) 回投げたときの結果の列と見なせます。そして、 \(n\) 回のコイントスの結果の列から \(i\) 回目の結果への関数 \(X_i: \Omega \to \lbrace 0,1 \rbrace\) は確率変数となります。また、 \(S = X_1 + \cdots + X_n\) は \(n\) 回のコイントスで表が出た回数を表す確率変数となります。
確率変数として、ある標本空間 \(\Omega\) から実数 \(\mathbb{R}^n\) への関数を考えることができ、この確率変数を多次元確率変数と呼びます。この資料では、多次元確率変数も単に確率変数と呼ぶことにし、多次元確率変数として、ある標本空間 \(\Omega\) からバイナリ列の集合 \(\lbrace 0,1 \rbrace^*\) への関数を考えることがあります。例えばバイナリ列 \(01011\) が出現する確率が \(\frac{1}{2}\) となるときに \(\operatorname{Pr}[X = 01011] = \frac{1}{2}\) と表すといった使い方をします。
確率変数 \(X\) から確率分布 \(p\) に従ってサンプル \(x\) を一つ取り出すことを \(x\leftarrow X\) と表記し、一様ランダムにサンプル \(x\) を一つ取り出すこと明示したい場合は \(x \stackrel{\$}{\leftarrow} X\) と表記します。また簡略して、確率変数ではなくその標本集合を使って、 \(x \leftarrow \Omega\) と書く場合もあります。
\(I\) を可算集合とします。確率変数の族 \(X=\lbrace X_i \rbrace_{i\in I}\) を集合 \(I\) でインデックスされたアンサンブルと呼びます。ここで、 \(X_i\) が確率変数です。例えば、上記の \(n\) 回のコイントスにおいて、 \(I=\lbrace 1,\ldots,n\rbrace\) としたアンサンブル \(X=\lbrace X_i \rbrace_{i \in I}\) を考えることができます。また、集合 \(I\) にバイナリ列を設定することがあります。その場合、アンサンブルは \(X=\lbrace X_w \rbrace_{w \in \lbrace 0,1 \rbrace ^n }\) などと表します。
識別不可能性
識別不可能性(indistinguishability)とは、二つのアンサンブルを見分けられない性質です。見分ける主体の能力と観測する値の数にどういった仮定を設定するかによって、パーフェクト識別不可能性・統計的識別不可能性・計算量的識別不可能性の3つパターンの定義付けが可能です。パーフェクト > 統計的 > 計算量的の順に識別不可能の度合いが緩くなります。それぞれ説明します。
以下、アンサンブル \(X = \lbrace X_w\rbrace_{w \in \lbrace 0,1 \rbrace^n},\ Y = \lbrace Y_w\rbrace_{w \in \lbrace 0,1 \rbrace^n}\) を考えます。
パーフェクト識別不可能性(perfect indistinguishability)
次の式を満たすとき、アンサンブル \(X\) とアンサンブル \(Y\) はパーフェクト識別不可能であるという。
簡単に言うと、どれだけ計算能力があっても、どれだけの値を観測したとしても、与えられたアンサンブルがどちらであるか見分けることができないという性質です。
パーフェクト識別不可能性は日本語の文献で完全識別不可能性と呼ばれることがありますが、後述する「perfect completeness」をこれに倣って訳すと「完全完全性」になって「頭痛が痛い」みたいになってしまうため、この資料では「perfect」をそのまま「パーフェクト」と訳すことにします。また、情報理論的識別不可能性とも呼ばれます。
統計的識別不可能性(statistical indistinguishability)
次の式を満たすとき、アンサンブル \(X\) とアンサンブル \(Y\) は統計的識別不可能であるという。
簡単に言うと、どれだけ計算能力があっても、多項式個の値を観測しただけでは、与えられたアンサンブルがどちらであるか見分けることができないという性質です。
計算量的識別不可能性(computational indistinguishability)
任意の確率的多項式時間アルゴリズム \(D\) に対して次の式を満たすとき、アンサンブル \(X\) とアンサンブル \(Y\) は計算量的識別不可能であるという。
簡単に言うと、確率的多項式時間アルゴリズムが、与えられたアンサンブルがどちらであるかを判断することが困難であるということです。確率的多項式時間アルゴリズムにとっては、計算量的識別不可能であるアンサンブルは同一であると見なせます。
以下、アンサンブル \(X\) とアンサンブル \(Y\) がパーフェクト識別不可能であることを \(X\equiv Y\) 、統計的識別不可能であることを \(X\equiv_s Y\) 、計算量的識別不可能であることを \(X\equiv_c Y\) と表記します。
一方向性関数、一方向性置換、ハードコア述語
一方向性関数とは、効率的に計算できる一方で逆関数は効率的に計算できない関数のことです。
一方向性関数(one-way function)
関数 \(f: \lbrace 0,1\rbrace^* \to \lbrace 0,1\rbrace^*\) が一方向性関数であるとは、以下の2つの条件を満たすことをいう。
1. ある多項式時間アルゴリズム \(A\) に対して次の式を満たす。
2. 任意の確率的多項式時間アルゴリズム \(A'\) に対して次の式を満たす。
ここで、 \(\lbrace 0,1\rbrace^n\) はアルファベット \(\lbrace 0,1\rbrace\) から作られる長さ \(n\) の文字列から成る言語で、 \(u\) はその言語から一様ランダムに選択された文字列で、 \(v\) はアルゴリズム \(A'\) に \(f(u\)) を入力したときの出力(文字列)である。条件2の式は \(f(u)\) と \(f(v)\) が一致する確率がnegligibleであることを意味する。
一方向性関数の存在は証明されていませんが、候補として以下の関数があります。
- RSA関数
- 有限体上のべき乗関数
- NP完全問題に基づく関数
また、 \(f(u)\) から \(u\) を効率的に計算することはできませんが、 \(u\) の部分情報を求めることは簡単である場合が多いです。しかし、 \(f(u)\) からどうしても求められない \(u\) の1ビットの情報が必ず存在することが知られています。この1ビットの情報のことを \(f\) のハードコア述語(hard-core predicate)と呼びます。述語(predicate)とは、出力が1ビットの関数のことです。ハードコア述語は形式的には次のように定義されます。
ハードコア述語
多項式時間で計算可能な述語 \(b:\lbrace 0,1 \rbrace ^* \to \lbrace 0,1 \rbrace\) に対して、 \(b\) が \(f\) のハードコア述語であるとは、任意の確率的多項式時間アルゴリズム \(A\) に対して、あるnegligibleな関数 \(\varepsilon\) が存在して、次の式が成り立つことをいう。
全単射写像を置換と呼ぶように、一方向性関数のうち全単射写像であるものを一方向性置換(one-way permutation)と呼びます。
確率的多項式時間Turingマシン
Turingマシンは計算機のモデルの一つです。その定義やイメージに関しては、他の文献を参照してもらうとして、ここではゼロ知識証明の文脈で必要な確率的多項式時間Turingマシンとそれに関する用語について簡単に説明します。
確率的Turingマシンは、非決定性Turingマシンの一種で、非決定性Turingマシンにおいて枝に確率が割り当てられたものと捉えることができます。また、確率的Turingマシンがある文字列を受理する確率は、確率的Turingマシンが次のどの枝を進むかどうかを確率的に決めていると捉えることができます。
「確率的Turingマシンが言語を認識する」とは、ある誤り確率 \(\epsilon\) のもとで、その言語に含まれる全ての文字列を受理し、その言語に含まれない全ての文字列を却下するということを意味します。すなわち、任意の \(w\) に対して、 \(w\in \mathcal{L}\) のとき \(w\) を受理する確率が \(1-\epsilon\) 以上で、 \(w\notin \mathcal{L}\) のとき \(w\) を却下する確率が \(1-\epsilon\) 以上であるということです。
確率的多項式時間Turingマシンとは、単に多項式時間で動作する確率的Turingマシンのことです。
2者間プロトコルの安全性とシミュレーションパラダイム
2者間プロトコル \(\Pi\) を、対話を行う確率的多項式Turingマシンの組 \((P_1,P_2)\) とします。文字列 \(x_1,x_2\) をそれぞれマシン \(P_1,P_2\) に対する入力とし、マシン \(P_1,P_2\) に \(x_1,x_2\) を与えられるとそれぞれ文字列 \(y_1 = P_1(x_1),y_2 = P_2(x_2)\) を出力するとします。
2者間プロトコルが安全であることを証明するにはどうしたらよいでしょうか。そのための手法の一つとして、シミュレーションパラダイムがあります。シミュレーションパラダイムとは、簡単に言えば、そのプロトコルが実現する機能を提供する信頼できるサードパーティー(trusted third party; TTP)がいる世界あったとして、敵対者の視点でどのように現実世界で振る舞ってもその世界で得られる情報と変わらないとき、そのプロトコルは安全であると証明する手法です。その世界のことを理想世界と呼びます。逆に正直なパーティー視点で言えば、現実世界で敵対者がどのように振る舞ってもその理想世界でTTPが教えてくれる情報と変わらないということです。
図で説明します。2者間プロトコル \(\Pi=(P_1,P_2)\) が実現しようとしている機能を \(\mathcal{F}\) とします。機能 \(\mathcal{F}\) を実行するTTPも \(\mathcal{F}\) と表すこととします。シミュレーションパラダイムのイメージとしては、下図において、任意の敵対者に対する現実世界(左)とある敵対者に対する理想世界(右)が変わらないことを証明することです。 図において \(A\) を現実世界の敵対者、 \(B\) を理想世界での敵対者とします。
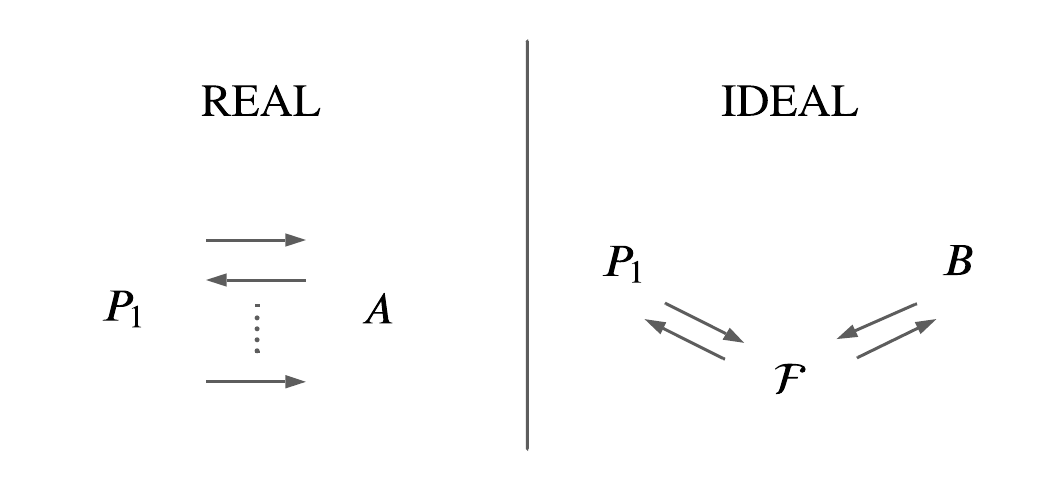
「どんな敵対者を考えた現実世界でも、ある一つの理想世界と同じだよね」と言えれば安全ということです。そうなるような敵対者 \(B\) をどう構成するのかが証明において大事になってきます。
もう少し形式的に説明していきます。機能 \(\mathcal{F}\) はパーティーへの入力 \(x_1,x_2\) を入力とし、パーティーの出力 \(y_1, y_2\) を出力する確率的Turingマシンです。つまり、マシン \(\mathcal{F}\) は2つのマシン \(P_1, P_2\) の振る舞いを再現します。
TTPである \(\mathcal{F}\) は、インフォーマルですが、誰とも結託せず公正に機能 \(\mathcal{F}\) を実行します。このとき、このTTP \(\mathcal{F}\) がいる理想世界ではプロトコル \(\Pi\) の安全な実行は簡単にできます。パーティー \(P_1,P_2\) はそれぞれの入力 \(x_1,x_2\) をTTP \(\mathcal{F}\) に渡し出力 \(y_1,y_2\) を得れば終わりです。
具体例として、じゃんけんプロトコル \(\Pi_{\mathrm{rsp}}\) を考えてみましょう。2者間プロトコルでじゃんけんを行うには工夫が必要ですが、プロトコル \(\Pi_{\mathrm{rsp}}\) が実現する機能 \(\mathcal{F_{\mathrm{rsp}}}\) を実行してくれるTTPが存在する場合、各パーティーがそのTTPにじゃんけんの手を与えて、TTPから勝ち負けの情報を得たら簡単にじゃんけんプロトコルを実現できることがわかります。ここで敵対者がいたとしてどのように行動しても不正行為ができないことは明らかです。敵対者ができる行動としては「グー」「チョキ」「パー」「それ以外」のどれかで、最後の一つは現実のじゃんけんと同様に負けとなるとします。「どれも与えない」という行動は、時間を考慮する場合に成り立つ行動なので考えません。TTPがじゃんけんの手を仲介するため、敵対者は相手の手を見てから自分の手を出すこと、いわゆる後出しができません。よって、TTPがいれば安全にプロトコルの実行ができることがわかります。
敵対者 \(A\) によって攻撃されたプロトコル \((A,P_2)\) あるいは \((P_1, A)\) の出力の確率変数を \(\mathrm{REAL}_{\Pi,A}(x_1,x_2)\) とします。これは、出力が \(y_1,y_2\) となる確率を \(p(y_1,y_2)\) として、
ということです。また、 \(x_1,x_2\) をパラメーターとする族を \(\mathrm{REAL}_{\Pi,A}\) とします。まとめると、次の式になります。
この理想世界において敵対者 \(B\) を考えてみましょう。敵対者 \(B\) はパーティー \(P_1,P_2\) どちらかの振る舞いをすることになります。 \(B\) が \(P_1\) の振る舞いをするとき、 \(B\) はまず \(x_1\) を受け取ります。 \(B\) はこの \(x_1\) から加工した情報 \(x_1'\) を作成できます。この \(x_1'\) を \(x_1\) の代わりに \(\mathcal{F}\) に与えることができます。すると、 \(\mathcal{F_i}\) を \(\mathcal{F}\) の出力の \(i\) 番目の項として、 \(\mathcal{F}\) が \(B\) に与える情報は \(\mathcal{F}_1 (x_1',x_2)\) となり、 \(P_2\) に与える情報は \(F_2(x_1',x_2)\) となります。よって、理想世界における出力は組 \((B(x_1, \mathcal{F}_1(x_1', x_2)), \mathcal{F}_2(x_1', x_2))\) です。同様にして、 \(B\) が \(P_2\) の振る舞いをするときの出力が求まります。
まとめると、理想世界における出力の確率変数 \(\operatorname{IDEAL}_{\mathcal{F},B}(x_1,x_2)\) は次のようになります。
そして、現実世界同様にこの確率変数の族を \(\mathrm{IDEAL}_{\mathcal{F},B}\) とします。
プロトコル \(\Pi\) が機能 \(\mathcal{F}\) を安全に実行できることは、プロトコル \(\Pi\) に対する任意の敵対者 \(A\) に対して、機能 \(\mathcal{F}\) に対するある敵対者 \(B\) が存在して、以下の式が成り立つことを示せば良いです。
敵対者 \(B\) の構成方法ですが、一般的な手法として \(B\) の内部で敵対者 \(A\) を利用して、その \(A\) に対して正直なパーティーをシミュレートするというものがあります。イメージとしては次のようになります。
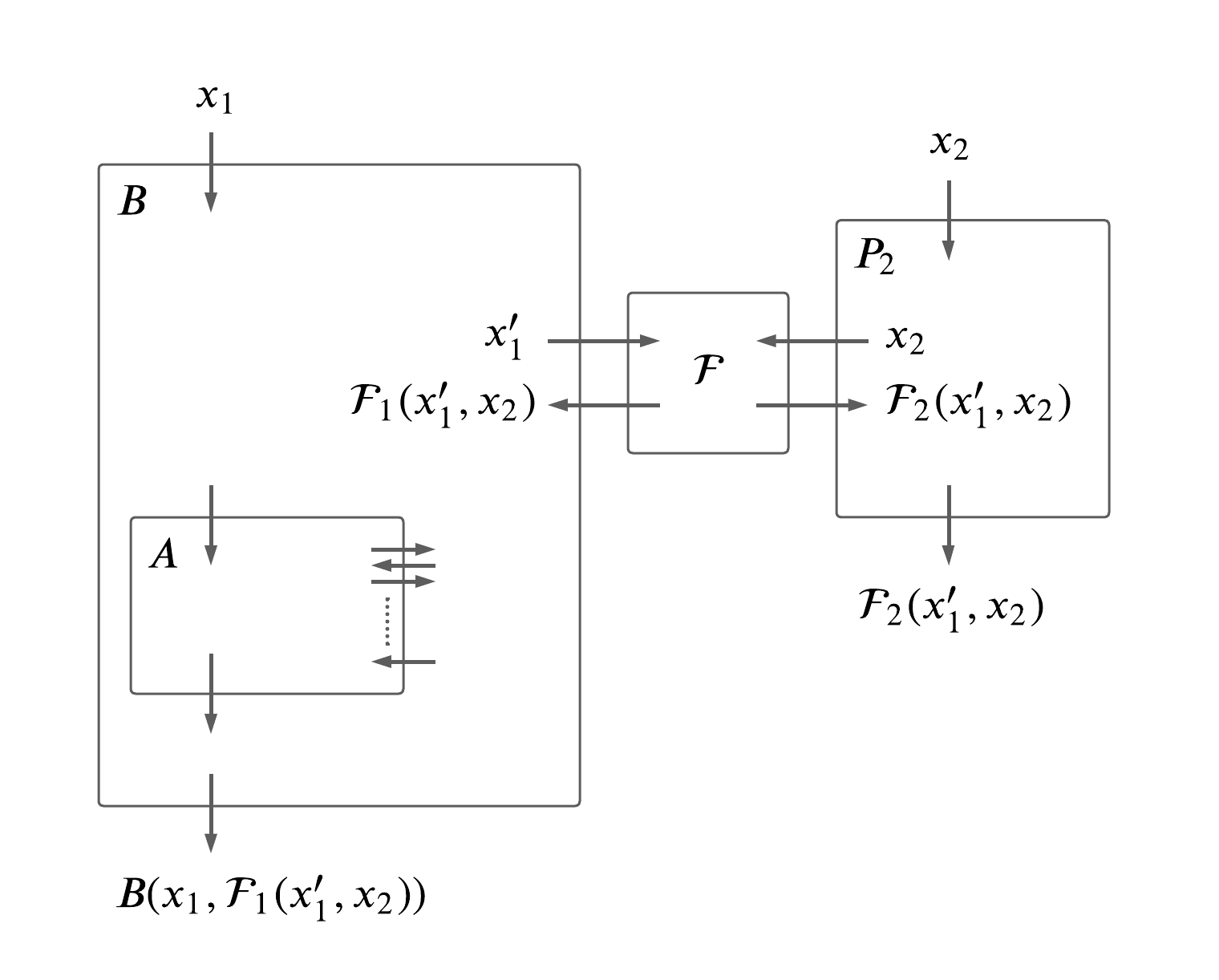
なぜこれで上手く \(B\) を構成できるかというと、インフォーマルには \(B\) の内部で \(A\) を利用することで現実世界の確率分布を理想世界に持ってくることができ、その理想世界の確率分布が現実世界の確率分布と変わらないよね、という主張が作れるからです。このような構成にして、この理想世界における出力 \((B(x_1,\mathcal{F}_1(x_1',x_2)), \mathcal{F}_2(x_1',x_2))\) が現実世界の出力 \((A(x_1),P_2(x_2))\) と変わらないことを示せれば良いということです。 \(B\) が正直なパーティーのシミュレートをすることから、 \(B\) をシミュレーターと呼ぶことがあります。
計算複雑性クラス
計算複雑性クラスとは、言語の判定に必要な計算量で言語を分類したときの言語の集合のことです。ここでは計算複雑性クラス \(\mathrm{P},\mathrm{NP},\mathrm{BPP}\) について説明します。
クラス \(\mathrm{P}\) は \(x\) を文字列として、 \(x \in \mathcal{L}\) かどうかを \(|x|\) の多項式時間で決定できるアルゴリズムが存在する言語 \(\mathcal{L}\) のクラスです。
クラス \(\mathrm{P}\) とは、 \(x,w\) を文字列として、 \(w\) が \(x\in\mathcal{L}\) の有効なウィットネスであるかどうかを \(|x|\) の多項式時間で決定できるアルゴリズムが存在する言語 \(\mathcal{L}\) のクラスです。 \(\mathrm{NP}\) において \(w\) を長さ0の文字列と考えると、 \(\mathrm{P}\) と同じと捉えられます。クラス \(\mathrm{P}\) は明らかに \(\mathrm{NP}\) に含まれますが、 \(\mathrm{NP}\) が \(\mathrm{P}\) に含まれるかは未解決問題です。
要は、 \(\mathrm{P}\) と \(\mathrm{NP}\) は次のようにまとめられます。
- \(\mathrm{P}\) は、言語の要素であることを多項式時間で判定できる言語の集合
- \(\mathrm{NP}\) は、言語の要素であることを補助情報を使えば多項式時間で判定できる言語の集合
\(\mathrm{P}\) と \(\mathrm{NP}\) をTuringマシンを使った定義は次のようになります。まず、 \(\mathbb{R}^+\) を \(0\) より大きい実数の集合とします。関数 \(t:\mathbb{N} \to \mathbb{R}^+\) において、Turingマシンで \(O(t(n))\) 時間で判定できる全ての言語の集合を、 \(\operatorname{TIME}(t(n))\) と定義します。また、非決定性Turingマシンで \(O(t(n))\) 時間で判定できる全ての言語の集合を、 \(\operatorname{NTIME}(t(n))\) と定義します。 \(\mathrm{P}\) と \(\mathrm{NP}\) は以下の数式で定義されます。
\(\mathrm{NP}\) において、非決定性Turingマシンを使った定義と、最初のウィットネスを用いた説明は等価であることが証明できますが、ここでは省略します。
クラス \(\mathrm{BPP}\) (bounded-error probabilistic polynomial timeの略)は、確率的多項式時間Turingマシンによる \(w\in \mathcal{L}\) の判定の誤りを確率 \(\frac{1}{3}\) で許す言語 \(\mathcal{L}\) のクラスです。誤り確率の \(\frac{1}{3}\) という値が中途半端だと思われるかもしれませんが、この値は \(0\) より大きく \(\frac{1}{2}\) 未満の値であればどんな値でもよく、それらが等価であることが次の増幅補題(amplification lemma)によって示せます。
増幅補題
\(\epsilon\) を \(0\) より大きく \(\frac{1}{2}\) 未満の定数である誤り確率とし、 \(\operatorname{poly}(n)\) を \(n\) の多項式とする。誤り確率 \(\epsilon\) の確率的多項式時間Turingマシン \(M\) を用いて、誤り確率 \(2^{-\mathrm{poly(n)}}\) の等価な確率的多項式時間Turingマシン \(M'\) を構築できる。
増幅補題の証明は省略しますが、簡単なイメージとしては、マシン \(M\) を複数回独立に動作してその結果の多数決をとることでマシン \(M'\) を構成できるというものです。例えば、ある文字列が言語に含まれ、マシン \(M\) がその文字列を受理すべきときに、マシン \(M\) を3回実行して多数決を取った結果の確率は、次のように計算できます。ここで、「o」が正しく受理したことを、「x」が誤って却下したことを表します。
| 1回目 | 2回目 | 3回目 | 多数決 | 確率 |
|---|---|---|---|---|
| o | o | o | o | \(\displaystyle \frac{2}{3}\cdot \frac{2}{3} \cdot \frac{2}{3} = \frac{8}{27}\) |
| o | o | x | o | \(\displaystyle \frac{2}{3}\cdot \frac{2}{3} \cdot \frac{1}{3} = \frac{4}{27}\) |
| o | x | o | o | \(\displaystyle \frac{2}{3}\cdot \frac{1}{3} \cdot \frac{2}{3} = \frac{4}{27}\) |
| x | o | o | o | \(\displaystyle \frac{1}{3}\cdot \frac{2}{3} \cdot \frac{2}{3} = \frac{4}{27}\) |
| o | x | x | x | \(\displaystyle \frac{2}{3}\cdot \frac{1}{3} \cdot \frac{1}{3} = \frac{2}{27}\) |
| x | o | x | x | \(\displaystyle \frac{1}{3}\cdot \frac{2}{3} \cdot \frac{1}{3} = \frac{2}{27}\) |
| x | x | o | x | \(\displaystyle \frac{1}{3}\cdot \frac{1}{3} \cdot \frac{2}{3} = \frac{2}{27}\) |
| x | x | x | x | \(\displaystyle \frac{1}{3}\cdot \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{27}\) |
多数決の結果が誤る確率は \(\frac{2}{27}\cdot{3} + \frac{1}{27} = \frac{7}{27}\) となることがわかります。これはマシン \(M\) の誤り確率 \(\frac{1}{3} = \frac{9}{27}\) より小さい値です。動作させる回数を増やしていけば、誤り確率が減少していくことが直感的にわかると思います。そしてこの誤り確率の減少は動作回数に対して指数的であることが証明できます。
関係、二項関係、NP関係
関係(relation)
\(A\) を集合とする。定義域を \(k\) 個の集合の組 \(A\times \cdots \times A\) として、値域を \(\lbrace\mathrm{TRUE}, \mathrm{FALSE}\rbrace\) とする関数 \(R\) を、関係という。特に \(k=2\) のとき、二項関係(binary relation)という。
関係は定義域の部分集合のように表記することがあります。例えば、定義域を \(\lbrace0,1\rbrace^* \times \lbrace0,1\rbrace^*\) とするある二項関係 \(R\) を \(R \subseteq \lbrace0,1\rbrace^* \times \lbrace0,1\rbrace^*\) と表します。また、 \(R(x,y) = \mathrm{TRUE}\) であることを、 \((x,y) \in R\) と表記します。
計算理論において二項関係はよく出てきます。例えば、探索問題は、入力となる文字列 \(x \in \lbrace0,1\rbrace^*\) が与えられたとき、何かしらの関係にある \(y\in \lbrace0,1\rbrace^*\) を計算する問題と考えることができ、これは二項関係 \(R \subseteq \lbrace0,1\rbrace^* \times \lbrace0,1\rbrace^*\) として考えられます。
さらに、NP探索問題も二項関係によって定義付けることができます。 文字列 \(x,w\) を与えて、 \((x,w) \in R\) かどうかを判定する多項式時間アルゴリズムが存在して、 \((x,w) \in R\) ならば \(|w| \le p(|x|)\) となるような多項式 \(p\) が存在するとき、関係 \(R\) はNP探索問題であると定義します。このとき、関係 \(R\) をNP関係と呼びます。ここで、 \(w\) をウィットネスと呼ぶことがあります。
算術回路
算術回路(arithmetic circuit)とは、多項式を計算するためのモデルであり、ラベル付きの有向非巡回グラフ(directed acyclic graph; DAG)を構成します。入力を入次数0のノードとし、その他のノードは \(+\) あるいは \(\times\) でラベルが付けられ、そのノードに入る有向辺の始点の多項式を、 \(+\) なら加算、 \(\times\) なら乗算します。出力は、インフォーマルには最後に計算されるノードの計算結果であり、そのノードを出力ノードと呼びます。ノードのことをゲート、有向辺のことをワイヤー、出力ノードから伸びるワイヤーを出力ワイヤーと呼びます。
下図は、算術回路の例です。多項式 \(x^3+x+5\) を計算した結果が \(35\) であることを示しています。
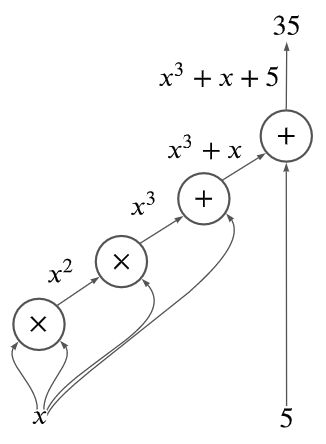
回路充足可能性(circuit satisfiability)問題は、ある回路が充足可能かどうかを判定する問題であり、論理回路の場合は論理回路充足可能性問題(CIRCUIT-SAT)、算術回路の場合は算術回路充足可能性問題と呼ばれます。どちらもNP完全です。
双線形群
この資料では、双線形群 \((p, \mathbb{G}_1, \mathbb{G}_2, \mathbb{G}_T, e, g, h)\) を扱います。ここで、 \(\mathbb{G}_1, \mathbb{G}_2, \mathbb{G}_T\) は位数が素数 \(p\) の群であり、写像 \(e:\mathbb{G}_1\times\mathbb{G}_2\to\mathbb{G}_T\) はペアリング(双線形写像)であるとします。また、 \(g,h,e(g,h)\) をそれぞれ \(\mathbb{G}_1,\mathbb{G}_2,\mathbb{G}_T\) の生成元とします。
双線形群には \(\mathbb{G}_1 = \mathbb{G}_2\) の対称双線形群と \(\mathbb{G}_1 \neq \mathbb{G}_2\) の非対称双線形群があります。また、対称双線形群はType Ⅰと呼ばれ、非対称双線形群のうち、効率的に計算できる同型性 \(\mathbb{G}_2 \to \mathbb{G}_1\) が存在するものはType Ⅱと呼ばれ、 \(\mathbb{G}_1\) と \(\mathbb{G}_2\) の間に効率的に計算できる同型性が存在しないものはType Ⅲと呼ばれます。非対称双線形群のうち両方向に効率的に計算できる同型性が存在するものは、対称双線形群と同じと見なせるため考えません。これら双線形群におけるペアリングは、単に「対称ペアリング」「非対称ペアリング」「Type Ⅰペアリング」「Type Ⅱペアリング」「Type Ⅲペアリング」などと呼ばれます。また、Type ⅠからType Ⅲの中で、Type Ⅲにおける演算は最も効率が良く、Groth16ではType Ⅲが使われています。
表記を簡単にするために、群の元の離散対数表記を導入します。 \(g^a\) を \([a]_1\) 、 \(h^b\) を \([b]_1\) 、 \(e(g,h)^c\) を \([c]_T\) と表記します。このとき、 \(g=[1]_1,h=[1]_2,e(g,h)=[1]_T\) となり、単位元は \([0]_1,[0]_2,[0]_T\) となります。加えて、群の元からなるベクトルを \([\boldsymbol a]_1\) のように太字で表します。