Quadratic Arithmetic Program
Groth16は、NP完全問題である算術回路充足可能性問題に対するzk-SNARKです。この算術回路充足可能性問題のステートメントを、Quadratic Arithmetic Program (QAP)と呼ばれる形式で考えることで非常に効率的に動作します。これは、従来の確率的検査可能証明(probabilistically checkable proof; PCP)を利用する手法より効率的です。VitalikのQAPの解説を参考に、SageMathで実際にステートメントをQAPに変換する例を見ていきましょう。
例として、ステートメントを「 \(p=101\) とする有限体 \(\mathbb{F}_p\)において \(x^3 + x + 5 = 35\) の解を知っていること」とします。解の一つは \(3\) です(有限体なので他に \(36,62\) があります)。左辺の \(x\) の多項式から出力outを生成することをSageMathのコードで表すと、次のようになります。
out = x^3 + x + 5
Flattening
この式にFlatteningと呼ばれる変換を行います。Flatteningはステートメントを算術回路として表現するために行います。具体的には、 x = y あるいは x = y (op) z という形式の処理の列に変換します。ここでy,zは変数あるいは数値、opは+,-,*,/のいずれかとします。実際に上記のコードにFlatteningを行うと次のコードが生成されます。
x2 = x * x
x3 = x2 * x
x3_x = x3 + x
out = x3_x + 5
結局Flatteningがやっていることは、ある計算(今回は \(x^3+x+5\) )を算術回路の表現にしているだけです。上記コードを算術回路として図に表すと次のようになっています。
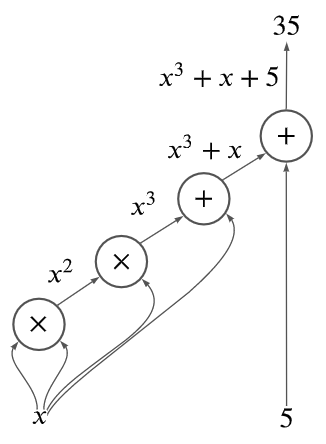
Rank 1 Constraint Systemへの変換
次に、このFlatteningされた表現(すなわち算術回路)からRank 1 Constraint System (R1CS)と呼ばれる形式に変換します。R1CSは3つのベクトルの組 \((a,b,c)\) の集合です。R1CSの各元 \((a,b,c)\) が上記コードの一行、すなわちゲートを表します。ここで全てのゲートに対して \((w\cdot a)(w\cdot b) - w\cdot c = 0\) を満たすような解 \(w\) をウィットネスと呼びます。
ベクトルの次元は変数の数と一致します。各次元に対応する変数を順に、数値 \(1\) を表すダミー変数 \(\mathrm{one}\) 、入力を表す変数 \(x\) 、出力を表すダミー変数 \(\mathrm{out}\) 、中間変数 \(\mathrm{x2},\mathrm{x3},\mathrm{x3\_ x}\) とします。よって次元は \(6\) で、ウィットネス \(w\) は次のイメージになります。
解 \(3\) のときのウィットネス \(w\) は次のようになります。
1つ目のゲートは、x2 = x * x に対応し、
となります。すなわち、
が \(\mathrm{x} \times \mathrm{x} - \mathrm{x2}\) となり、この式に実際にウィットネスの値を代入すると \(0\) となっています。
同様に4つの全てのゲートに対して、 \(a,b,c\) が求まります。各ゲートの \(a\) を列として並べた行列を \(A\) とし、 \(b,c\) に対しても同様に \(B,C\) とすると、
となり、これが今回のステートメントに対するR1CSです。
QAP還元
R1CSをQAPに変換します。この変換はQAP還元(QAP reduction)と呼ばれます。変換のイメージは、上記の行列の全ての行に対して、その行を一つの多項式に圧縮する処理です。
具体例を見ていきます。 \(A\) の1行目 \((0,0,0,5)\) を多項式補間の一つであるLagrange補間を使って多項式に変換します。この行の \(x\) 番目の要素を \(y\) として、点 \((x,y)\) を考えます。添字は1から始めます。点 \((1,0),(2,0),(3,0),(4,5)\) を全て通る多項式をLagrange補間を利用して求めます。
R.<x> = PolynomialRing(GF(101), 'x')
f = R.lagrange_polynomial([(1,0),(2,0),(3,0),(4,5)])
print(f"{f=}")
print(f"{f(1),f(2),f(3),f(4)=}")
結果は次のようになります。
f=85*x^3 + 96*x^2 + 26*x + 96
f(1),f(2),f(3),f(4)=(0, 0, 0, 5)
同様に、 \(A,B,C\) の全ての行に対してLagrange補間を行い多項式を生成します。行列 \(A,B,C\) の変換後はベクトルとなり、それぞれ \(a',b',c'\) と表すとすると次のようになります。
これがQAPです。次のコードで求めました。
def gen_lagrange_polynomials(A):
N = len(A)
M = len(A[0])
polys = []
for j in range(M):
points = [(i + 1, A[i][j]) for i in range(N)]
polys.append(R.lagrange_polynomial(points))
return polys
A = [[0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0], [0, 1, 0, 0, 1, 0], [5, 0, 0, 0, 0, 1]]
B = [[0, 1, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0]]
C = [[0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 1], [0, 0, 1, 0, 0, 0]]
ap = vector(gen_lagrange_polynomials(A))
bp = vector(gen_lagrange_polynomials(B))
cp = vector(gen_lagrange_polynomials(C))
QAPのチェック
R1CSをQAPに変換することで何ができるようになったかと言うと、R1CSの制約を個々にチェックすることなく、全ての制約を同時にチェックできるようになったことです。
多項式 \((w\cdot a')(w\cdot b') - w\cdot c'\) を考えます。この多項式を \(x=1,2,3,4\) のどれかで評価すると \(0\) になります。つまり、この多項式は、 \(h(x)\) を適当な多項式として、 \((x-1)(x-2)(x-3)(x-4)h(x)\) の形で表せるので、 \(X\) を \(1,2,3,4\) ではないある定数(不定元)として、 \((X-1)(X-2)(X-3)(X-4)\) で割り切れます。これを利用して、もし割り切るなら正当なウィットネスであり、もし割り切れなければウィットネスが間違っていると判定できます。
実際にSageMathで確認してみます。
z = (x-1)*(x-2)*(x-3)*(x-4)
w = vector([1, 3, 35, 9, 27, 30])
f = w.dot_product(ap) * w.dot_product(bp) - w.dot_product(cp)
f.quo_rem(z)
(19*x^2 + 90*x + 30, 0)
となり、余りが \(0\) になっていることがわかります。ちなみにf.roots()は[(4, 1), (3, 1), (2, 1), (1, 1)]となっています。
QAPの形式化
QAPを形式的に記述します。まず、有限体 \(\mathbb{F}\) 上で、加算ゲートと乗算ゲートからなる算術回路を考えます。ゲートを一般化すると、次の方程式で表すことができます。
ここで、 \(a\) はワイヤーを表す変数で、 \(a_0 = 1,\ a_1,\ldots,a_m \in \mathbb{F}\) です。また、 \(u,v,w\) はゲートの動作を定義する定数であり、 \(u_i,v_i,w_i \in \mathbb{F}\) です。 \(m\) はワイヤーの本数であり、適当な正整数です。ワイヤーはステートメントワイヤーとウィットネスワイヤーで構成されています。
では、加算ゲートと乗算ゲートがこの方程式のどのような特殊ケースであるかを見ていきましょう。まず、乗算ゲートは、適当な定数 \(i,j,k\) を利用して \(a_i\cdot a_j = a_k\) と表すことができます。 \(i\) 番目のワイヤーの値と \(j\) 番目のワイヤーの値を掛けた結果を \(k\) 番目のワイヤーの値として返す乗算ゲートだということです。イメージは次のようになります。

このように表した乗算ゲートは、上記の一般化したゲートの方程式において、
となるようにしたときの、 \(a_i\cdot a_j = a_k\) です。ここで、 \(u_i=v_j=w_k=1\) であり、他の定数は \(0\) となっています。
また、加算ゲートは、適当な定数 \(i,j,k\) を利用して、
となるようにしたときの、 \(a_{i} + a_{j} = a_k\) と表せます。
上記の一般化したゲートの方程式は一つのゲートを表すものですが、前のセクションと同様に、一つの方程式で複数のゲートをまとめて表せるようにしましょう。多項式補間を使います。
まず、有限体 \(\mathbb{F}\) から \(n\) 個の異なる元 \(r_1,\ldots,r_n\) を選びます。 \(u_i(x),v_i(x),w_i(x)\) を、 \(i\) を \(0\) 以上 \(m\) 以下の整数、 \(q\) を \(1\) 以上 \(n\) 以下の整数として、任意の \(i,q\) に対して次の式を満たすような、次数 \(n-1\) の多項式とします。
これら多項式は、多項式補間によって求めることができます。これら多項式を用いて、算術回路における \(q\) 番目のゲートを、次の式で表すことができます。
よって、次の方程式は \(q\) 個のゲートをまとめて表現できています。
前のセクション同様に、次の多項式は、多項式 \(t(x) = \Pi_{q=1}^n(x-r_q)\) を因子に持ちます。
つまり、適当な多項式 \(h(x)\) を利用して、次の方程式が成り立ちます。
ここで、多項式 \(u_i(x),v_i(x),w_i(x)\) が次数 \(n-1\) であるので、左辺の次数は \(2(n-1)\) になります。多項式 \(t(x)\) の次数は \(n\) なので、多項式 \(h(x)\) の次数は \(n-2\) になります。
\(X\) を \(\forall q,\ X\neq r_q\) を満たすある定数(不定元)として、上記方程式を \(t(X)\) で剰余を取れば、次の式が成り立ちます。
以上の定義を利用して、QAPを次のように記述される組 \(R\) として定義します。
ここで、 \(\mathbb{F}\) は有限体であり、 \(m\) はワイヤーの本数であり、 \(\ell\) はステートメントワイヤーの本数で \(1\le \ell \le m\) です。また \(\mathrm{aux}\) は補助情報(auxiliary information)とします。補助情報 \(\mathrm{aux}\) には何を指定するかというと、例えば、ペアリングに基づく非対話型ゼロ知識アーギュメントを考えているのであれば双線形群を指定します。
このQAP \(R\) は以下の二項関係を定義し、この関係も \(R\) として表します。
ここで、 \(\phi\) は \(\ell\) 個のステートメントワイヤーの列、 \(w\) は \(m-\ell\) 個のウィットネスワイヤーの列を表しており、それら \(\phi,w\) が \(\displaystyle\sum_{i=0}^m a_i u_i(X) \cdot \displaystyle\sum_{i=0}^m a_i v_i(X) \equiv \displaystyle\sum_{i=0}^m a_i w_i(X) \mod t(X)\) を満たすときに限り、組 \((\phi,w)\) が \(\mathrm{TRUE}\) となるような関係が \(R\) であるということです。